凸包相关

定义

通常说的凸包是指一个点集的凸包，并且是指在二维平面上¹。这种凸包本身是一个凸多边形，由点集中的点构成，并且要求凸包上的点尽可能少。下面是一个凸包的示例：

convex-hull-example-1

对于其它的图形，也可以有凸包，如线段的凸包：

convex-hull-example-2

实际上线段的凸包就是所有线段的端点的凸包。更一般的，多边形的凸包就是所有多边形的顶点的凸包。

而曲线图形的凸包则没有这么简单，从圆的凸包就可见一窥：

convex-hull-example-3

下面的文章将不讨论与曲线相关的凸包。

特别的，当点集里只有两个点时，凸包退化为一条线段。只有一个点时，退化为一个点。
同时需要注意多点共线和多点重合而导致的凸包退化现象。

构造算法

在计算几何里面，计算凸包就跟排序一样十分经典，至今已经研究出了许多算法。它们中的绝大部分可以在维基百科上看到，这里只介绍Javis步进法、水平扫描线法和Graham扫描法。

Jarvis步进法 (Gift Wrapping)

Jarvis步进法可以看作是给点集包上包装纸，最后算出凸包的。算法过程非常简单：

找出最左下和最右上的两个点，记为$p_1$、$p_2$，它们一定是凸包上的点。
设$p_1$为当前点，每次从剩下的点中找出以当前点为原点极角最小的点，将其加入凸包，并设为当前点。重复这一步骤，直到遇到$p_2$。这样完成了凸包右边的构造。
与第二步相似，构造凸包的左边（每一步寻找极角最大的点）。

以下面的点集为例：

jarvis-1

首先找到左下和右上两个点：

jarvis-2

构建右凸包：

jarvis-3
jarvis-4

构建左凸包：

jarvis-5
jarvis-6
jarvis-7

至此，凸包构建完毕。

由于Jarvis步进法中凸包每一个点都需要对剩下的点进行处理，所以该算法的时间复杂度为$\Theta(nh)$，其中$h$是凸包的规模。最坏情况下为$\Theta(n^2)$。由于当点在一个有限矩形内随机分布时凸包的期望规模为$O(\log n)$，所以在这种情况下，该算法的时间复杂度为$O(n\log n)$。

下面是其伪代码：

function JARVIS(Q):  # Q是点集
    if |Q| <= 3:  # 点数不大于3
        return Q

    p1, p2 = nil
    for p in Q:
        if p1 == nil or ( p.y < p1.y or p.y == p1.y and p.x < p1.x ):
            p1 = p
        if p2 == nil or ( p.y > p2.y or p.y == p2.y and p.x < p2.x ):
            p2 = p

    # 使用叉积来比较极角大小
    CH = [p1, p2]  # 凸包
    Q.pop(p1, p2)  # 删除p1, p2

    # 右凸包
    x = p1
    while true:
        y = Q[0]
        for p in Q[1:]:
            if cross(y - x, p - x) < 0 or
               cross(y - x, p - x) == 0 and |y - x| < |p - x|:  # 共线
                y = p

        if y == p2:
            break

        CH.append(y)
        Q.pop(y)
        x = y

    # 左凸包
    x = p1
    while true:
        y = Q[0]
        for p in Q[1:]:
            if cross(y - x, p - x) > 0 or
               cross(y - x, p - x) == 0 and |y - x| < |p - x|:  # 共线
                y = p

        if y == p2:
            break

        CH.append(y)
        Q.pop(y)
        x = y

    return CH

水平扫描线法

计算几何中，扫描线是一种常用的方法。我们也可以使用扫描线来计算凸包。
我们可以从左至右扫描每一个点来更新凸包。可以确定，最左边和最右边的点都是凸包上的点。因此利用扫描线来分别计算上下凸包。
算法步骤如下：

将所有点按照$x$排序。
对于每一组$x$相同的点，仅保留$y$值最大和最小的点。
取出最左和最右作为基点，用于判断其它的点是在上凸包还是下凸包。
从左至右扫描每一个点，根据基点利用叉积计算该点是应插入上凸包还下凸包，将其插入对应的凸包中。然后从这个点开始向前访问，如果和之前的点形成内凹的形状（可以利用叉积判断），就将之前的点删除。直到不存在这样的形状为止。

下面展示了一个水平扫描线的示例：

scanline-1
scanline-2
scanline-3
scanline-4
scanline-5
scanline-6
scanline-7
scanline-8
scanline-9
scanline-10
scanline-11
scanline-12
开始从上凸包中删除点：

scanline-13
scanline-14
scanline-15
scanline-16
scanline-17

由于每个点只会被访问1次，点在栈中只会被弹出一次，所以扫描线的部分是$\Theta(n)$的。但排序需要$O(n\log n)$的时间，所以总复杂度是$O(n\log n)$的。是一个非常不错的算法。

伪代码如下：

function SCANLINE(Q):
    if |Q| <= 3:
        return Q

    sort Q by order of x
    foreach x keeps the highest and lowest points

    p1, p2 = Q[0], Q[-1]
    CH1 = []
    CH2 = []
    for p in Q:
        if p == p1:  # 起点
            CH1.append(p)
            CH2.append(p)
            continue
        if p == p2 or  # 终点
           cross(p2 - p1, p - p1) >= 0:  # 在上凸包
            while |CH1| > 1 and cross(CH1[-1] - CH1[-2], p - CH1[-2]) >= 0:
                CH1.pop()
            CH1.append(p)
        if p == p2 or
           cross(p2 - p1, p - p1) < 0:  # 在下凸包
            while |CH2| > 1 and cross(CH2[-1] - CH2[-1], p - CH2[-2]) <= 0:
                CH2.pop()
            CH2.append(p)

    merge CH1, CH2 into CH
    return CH

Graham扫描法

计算凸包的另外一种算法就是Graham扫描法，也可以视为是旋转扫描线的运用。类似于Jarvis步进法这种不断包裹形成凸包的方法，Graham扫描法首先选出一个肯定在凸包上的点作为基点，然后将其它点进行极角排序，按照极角序的顺序来扫描。并且按照水平扫描线算法中删除先前的点的方法来不断更新凸包。
Graham算法有一个好处，就是最终得到的凸包还是按照极角序排列的，不需要再次排序，方便后续的处理。

算法步骤如下：

选出最左下的点作为基点
以基点为原点，其它点按照极角逆时针排序。对于极角相同的点，保留与基点距离最远的点。
维护一个栈，依次访问每一个点，检查之前的点是否与其形成了凹陷的形状（利用叉积判断），如果有就从栈中退掉一个点。否则将该点压入栈中。
最后栈中元素就是凸包

下面给出了一个示例：

graham-1
graham-2
graham-3
graham-4
graham-5
graham-6
graham-7
graham-8
graham-9
graham-10
graham-11

图上依次连接的线表示栈中的元素。

对于Graham扫描法的时间复杂度，与水平扫描线的分析一致，关键在于排序的时间复杂度。
该算法总体复杂度为$O(n\log n)$。

下面是该算法的伪代码：

function GRAHAM-SCAN(Q):
    if |Q| <= 3:
        return Q

    select the base point p1

    sort Q by polar angle order, when meets the same polar angle,
    keep the furthest one.

    CH = []
    for p in Q[1:]:
        while |Q| > 1 and
              cross(Q[-1] - Q[-2], p - Q[-2]) <= 0:
            CH.pop()
        CH.append(p)

    return CH

小结

上面介绍了三种凸包构造算法，其中水平扫描线法和Graham扫描法是最为常用和高效的算法。
这两种算法中的扫描线方法可以被单独拿出来使用，因而可以做进一步扩展（如下面将提到的动态凸包问题）

扩展与应用

动态凸包

动态凸包是指要求实现动态插入点并维护点集凸包的问题，目前好像还没有支持在线²删除点的高效算法。
目前流行的两种动态凸包算法来源于之前的两种凸包算法：水平扫描线法和Graham扫描法。

水平序

第一种是来源于水平扫描线的算法。我们用两棵平衡树来维护上下两个凸包，均按照$x$排序。
每次插入点之前，先要判断点是否在凸包内部。首先二分出该点所在的上凸包或下凸包的左右两个点，然后利用叉积来判断是否在凸包外。注意这里有几个边界情况：

点超出了凸包的最左边和最右边时要单独处理。
点的$x$与最左边或最右边相同时需要考虑一下。

如果点在凸包内，那么凸包将不会被更新。否则就要考虑更新凸包。
按照同样的方法，在平衡树上查找出该点在凸包上左边和右边的点，然后向左向右检查是否有违反凸包性质的凹陷形状，如果有，则删除对应的点。直到凸包性质得到维护。然后将该点插入即可。
类似的，对于之前判断点是否在凸包内的边界情况，在这里就需要更加注意。
由于有上下两个凸包，所以相似的代码需要写两遍......

极角序

第二种是来源于Graham扫描法的算法，这个算法与水平序相比边界更简单，代码也更短。
该算法要求得到一个初始的凸包（至少两个点），并以这些点的中心作为原点，按照极角序³插入到平衡树中。
与水平序类似，首先要查询点是否在凸包内部。同样，我们在平衡树中查找极角左右的点，并利用叉积判断是否在凸包内。注意我们期望这些点会按照一个环的方式存入，然而平衡树是链状数据结构。因此在边界处需要到另外一边寻找答案。
如果查询的点与原点一样，就没有极角可言了，因此我们需要判断该点是否与原点一样。由于我们的原点必定在凸包内，所以可以直接判定。

之后的插入与水平序一致，二分出左右点，并维护凸包性质即可。
注意这里没有超出左右边界的情况，这就是极角序的一大优势。同时，极角序也只用维护一棵平衡树。

具体实现

[Codeforces 70D] Professor’s task

这道题是非常良心的模板题，如果想实现动态凸包，可以到这里来测试。
本人的代码由于是手写的向量和平衡树，所以代码相当长，就不在此以代码框的形式放出。有兴趣的可以点开下面的链接来看：

水平序
 极角序

旋转卡壳

旋转卡壳是一类应用于凸多边形上的算法。由于凸包也是凸多边形，所以也可以用在凸包上。
为了解释什么是旋转卡壳，首先来看一个经典的问题：

给你一个点集$Q$，求这个点集中最远⁴的两个点的距离。

该问题最为直接的方法是枚举这两个点对，然后计算距离。这样做的时间复杂度为$\Theta(n^2)$。
有没有一种更快的算法呢？首先可以注意到，最远的两个点一定在凸包上，因为如果它们不在凸包上，那么凸包实际上可以被扩大。
这样我们就只用考虑凸包上的点了。对于凸包上的一个点，很直观的想法就是找到凸包另一边最远的点。
这是就要用到旋转卡壳，我们用一对平行线”夹紧”这个凸包，这样被两条直线所压住的点之间就可能有最远点对。

ruler-1

由于当前所卡中的不一定就是最远点对，所以还需要继续寻找。
而对每一条凸包上的边而言，都只有最远的点对其有效。
所以可以想象其中一条直线不断的沿着凸包上的边进行旋转，而另一条直线则不断更新与之最远的点。

ruler-2

第一条直线的事情好办，关键在于第二条。由于凸包上的点到第一条直线的距离具有单调性，所以第二条直线可以沿着一个方向移动，从而到达合适的位置。
当然需要注意一种边界情况：如果有两条平行的边，那么第二条直线可能卡中两个点⁵，这样就需要多枚举一些情况。

按照这样的方法旋转一周，就可以对所有可能的点对完成枚举，极大地减少了枚举量。
对于凸多边形的每一条边我们都要计算一次答案。如果计算答案的复杂度为$O(g(n))$，那么旋转卡壳的复杂度就是$O(ng(n))$。对于最远点对问题，我们可以在$\Theta(n)$的时间内解决。

旋转卡壳还有许多有趣的应用，很多情况下是用于解决点集和凸多边形上的问题。

斜率优化

斜率优化是一类应用在递推优化上的算法，它巧妙在于将看似没有规律的递推关系转为了二维平面上的线性规划问题。下面举一个简单的例子：

给你一个数组$A[1\dots n]$和$B[1\dots n]$ $(A[i],\;B[i] > 0,\;i\in[1.\;n])$，并给出$f(1)$和$f(2)$，已知$f$具有以下递推关系：
$$ f(x) = \max\{A[x]f(i) + B[x]f(i - 1) \mid i \in [2,\;x)\} $$

求$\sum_{i=1}^nf(i)$。

首先，直接枚举的时间复杂度为$\Theta(n^2)$，并不是很优。
如果单纯是取最大值，这个问题就可以用线段树来解决。然而$\max$中的东西简直莫名其妙，令人摸不着头脑。
不妨从另外一个角度来考虑问题。对于当前的$x$而言，考虑之前的两个位置$j,\;k \in [2,\;x)$ (假定$j \lt k$)，什么时候$j$会比$k$更优（即可能取到最大值）。
我们发现。只有下面的不等式成立时，$j$会比$k$更优：
$$ A[x]f(j) + B[x]f(j - 1) \gt A[x]f(k) + B[x]f(k - 1) $$

由于$f(x)$是递增的，所以我们可以尝试对上式进行一些等价变形：
$$ A[x](f(j) - f(k)) \gt B[x](f(k - 1) - f(j - 1)) $$

$$ {f(j) - f(k) \over f(k-1) - f(j-1)} \gt {B[x] \over A[x]} \tag{1} $$

$$ {f(j) - f(k) \over f(j-1) - f(k-1)} \lt -{B[x] \over A[x]} \tag{2} $$

回想一下直线斜率的计算公式，不难发现$(2)$式左边是一个计算斜率的形式，而右边是一个常量（对特定的$x$而言）。
因此$(2)$式左边可以视为是两个点$(f(j-1),\;f(j))$和$(f(k-1),\;f(k))$的直线的斜率与$-B[x] / A[x]$的关系。

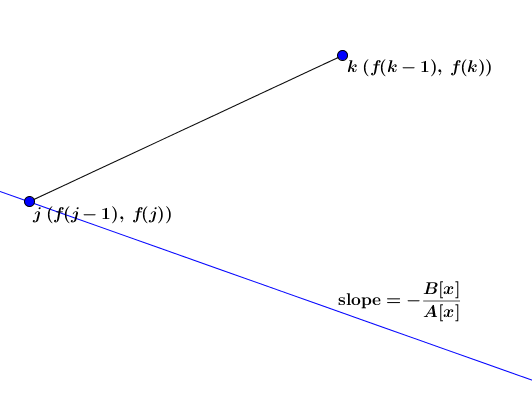
slope-opt-1

如上图所示，这个时候：
$$ {f(j) - f(k) \over f(j-1) - f(k-1)} \gt -{B[x] \over A[x]} $$

故此时$j$不比$k$更优。

可以注意到，对于这个问题，查询的斜率都是负数，所以只要两点间的斜率大于$0$，就可以有更优的调整。
因此所有非上凸包的点都不比上凸包的点更优。
于是我们就只用考虑上凸包的点了。
由于上凸包的相邻两点间斜率是递减的，而我们的目标是查找到第一个小于$-B[x] / A[x]$的边，所以我们可以采用二分的方法！
到此整个算法已经很妙了，只剩下一个问题，就是这些点并不是一开始就知道的。
所以我们需要动态插入点并维护凸包，这就需要之前所提及的动态凸包。
由于只需要上凸包，所以这里最好选用水平序，并且只需要维护一棵平衡树。

这样这个问题我们就做到的$O(n\log n)$的时间复杂度。

事实上，机智的人可能发现这个问题并不需要这种高级的方法，然而这里只是为了解释什么是斜率优化。在真正复杂的地方，斜率优化还是有很大用处，并且形式也多变。

凸包的定义可以扩展至高维。 ↩
如果只需要删除且允许离线，则可以进行”时光倒流”，从后往前处理，这样就变成了插入。 ↩
最好采用先象限后极角的方法，避免一些边界情况。 ↩
最近点对问题的解决方法与之完全不同，通常是采用分治法。 ↩
由于凸包上不允许出现同一条直线上出现多于两个点（因为要使凸包上的点尽可能少），所以不会同时卡中三个以上的点。 ↩